|
| Yβ=1-εβ | β |
≥Yβmin |
| 120° |
Yβmin=1-0.25εβ≥0.75
式中,当εβ>1时,按εβ=1计算;当Yβ<0.75时,取Yβ=0.75。
Yβ也可按GB3849—83图47查取。
弯曲强度的重合度系数
重合度系数Yε是将载荷由齿顶转换到单对齿啮合区上界点的系数。
对于1<εa<2的齿轮副可按下式计算:
![]()
齿面胶合强度计算
齿面胶合为齿轮常见失效形式之一。目前已把齿面抗胶合承载能力作为评价齿轮承载能力的第三个指标。
引起齿面胶合的因素较多,且错综复杂,发生胶合破坏的机理迄今还不十分清楚,因此齿面胶合强度计算,目前尚无成熟的统计一计算方法。从已经发表的计算方法来看,大体归纳为两大类:一类是以接触齿面间形成的润滑油膜来衡量齿轮传动的抗胶合强度,它包括以油膜厚度为准则和油膜强度为准则的两种方法;另一类以计算齿面间所产生的摩擦功作为衡量齿面胶合强度的准则,它包括直接计算摩擦功(如PV和PVT值法)和计算由摩擦功转化成齿面温升(如最大接触温度法——Bolok闪温法和平均温度法——积分温度法)。根据德国慕尼黑工业大学的齿轮与齿轮机构研究所(FZG)关于齿轮胶合的学术报告,认为对于齿轮的磨损与胶合计算,在低速(圆周速度v
<7m/s)时,可以油膜厚度为准则;在中速(v
<7~30m/s)时,可以用油膜强度或表面温度法;在高速(v>30m/s)时,要用表面温度法。
国际标准化组织(ISO)TC60/WG6工作组,于1980年提出两种齿面抗胶合承载能力计算法:闪温法和积分温度法。GB6413—86采用积分温度法,它主要针对齿面载荷和滑动速度引起的齿面高温导致润滑油膜破裂所造成的热胶合损伤。
油膜厚度
油膜厚度法是计算接触齿面间的油膜厚度,当最小油膜厚度hmin≥[hmin]=λ(Rx1+Rx2)
式中,λ为安全裕度,一般取λ=4;hmin为最小油膜厚度,可按Dowso-Higgison公式算出。
油膜强度法
润滑油及其添加剂在金属齿面上形成牢固粘附的边界膜(物理—化学保护膜),这层边界膜具有一定的抗胶合极限强度,如果设计齿轮的接触应力不超过这个极限值,则齿轮副就不会发生胶合。其表达式为:
| SB= | Pzul |
≥1.5 |
| Pw |
式中,SB为胶合强度的安全系数;Pw为齿轮的计算接触应力,按齿面接触应力公式计算;Pzul为润滑油膜的抗胶合许用接触应力,可按G.Lechiner公式计算。
PV值法
齿面上单位时间、单位接触面积上所消耗的摩擦功μPV将转变成热能,使齿面温度升高,润滑油粘度降低,破坏齿面润滑,导致胶合失效。因此,用齿面上PV的最大值作为确定齿面胶合强度的指标。齿面胶合的判据为:PV≤[PV]。
式中,P为啮合点的接触应力,按赫兹公式计算;V为啮合点的滑动速度(齿面速度之差);[PV]为许用PV值,根据试验决定。
PVT法
在齿轮啮合传动时,有强烈的摩擦热产生,导致齿面胶合破坏。J.O.Almen提出用于航空直齿和斜齿轮的胶合强度计算方法,其判据为:PVT≤[PVT]。式中,P为啮合点的接触应力,按赫兹公式计算;V为啮合点的滑动速度;T为啮合线上由节点到所计算啮合点的距离;[PVT]为许用值。
平均温度法
一个啮合循环中各啮合点的瞬时温升θfla求平均值θflaint(沿啮合线的积分平均温度),由于它和本体温度θM对胶合失效的影响不同,因此将其乘以加权系数C2再与本体温度相加,所得到的值称为齿面平均温度或积分温度θint。当此温度超过某一临界值θsint,就可能发生胶合失效。经过对各种润滑油所作大量试验证明,此临界胶合合温度θsint对任一种润滑油和齿轮材料组合,是一个大致不变的常数,它与运转条件无关。平均温度法的胶合判据为:
| θint≤θM+C2θflaint≤ | θsint |
或 SB= | ≥SBmin | |
| SBmin |
式中,SB为胶合承载能力计算安全系数;SBmin为胶合承载能力最小安全系数。
平均温度法又称积分温度法。它只适用于齿面载荷和滑动速度引起的齿面高温导致润滑油膜破坏所造成的热胶合损伤,且只限于重合度εa<2的齿轮传动,但可适用各种润滑油。
瞬时接触温度法
由于齿面间的滑动速度区摩擦产生的高温使润滑油膜破裂,局部金属直接接触,随后摩擦系数增大,导致高温金属焊合,在滑动速度作用下焊点被撕伤,形成胶合失效。因此,限制齿面上出现在啮合瞬间的最大接触温度,即可防止胶合失效。其判据为:
| θB=θM+θfla≤θS 或 SB= | ≤SBmin |
式中,θB为在一个啮合循环中,各啮合点瞬时接触温度中的最大值;θS为临界值;θM为齿面进入啮合区前的温度,称为本体温度或体积温度,对齿面上各啮合点为一常数;θfla为啮合瞬间由摩擦形成的局部温升,称为瞬时温升或闪温;θoil为润滑油温度;SB为胶合安全系数;SBmin为胶合强度计算允许的最小安全系数。
瞬时接触温度法又称最大接触温度法,或JBlok闪温法。目前瞬时接触温度计算方法很多,有的已纳入国家标准,如ISO、DIN、AGMA、库氏计算法等。
小齿轮齿顶几何系数
它是考虑小齿轮齿顶E处的几何参数对赫兹应力和滑动速度影响的系数,用XBE表示。可按GB6413—86式(23)求得。
齿顶修缘系数
它是考虑齿顶修缘(或修根)对胶合影响的系数,用Xca表示。可由GB6413—86图3查出。
热闪系数
它是考虑材料特性(弹性模量E、泊松比v、热接触系数BM)和两轮在啮合点处沿齿廓切线方向速度vp1、vp2之影响的系数,用XM表示。可按GB6413—86式(23)求得。
啮入冲击系数
它是考虑滑动速度较大的从动齿顶啮入冲击载荷之影响的系数,用XQ表示。可由GB6413—86表2查出。
润滑系数
它是考虑润滑方式对传热影响的系数。由试验得出:
油浴润滑时,XS=1.0;
喷油润滑时,XS=1.2。
材料焊合系数
它是考虑设计齿轮与试验齿轮的材料及表面处理不同而引入的修正系数,用XW表示。它是一个相对比值,由不同材料及表面处理的试验齿轮与标准试验齿轮进行对比得出。其值可由GB6413—86表4查取。
重合度系数
它是假设载荷全部作用在小齿轮齿顶时的局部瞬时温升折算成沿啮合线积分平均温升的系数,用Xε表示。可按GB6413—86式(29)、(30)、(31)计算。
瞬时温升
在啮合瞬间,啮合点由摩擦热形成的局部温升,称为瞬时温升或闪温,用θfla表示。在退出啮合后,此温升立即被润滑油冷却。由于齿面上各啮合点的滑动速度、几何参数、载荷等不同,故θfla也不相同。
积分平均温度
齿面各啮点瞬时温升,θfla沿啮合线的积分平均值,称为积分平均温度,用θflaint表示。
本体温度
轮齿即将进入啮合时的齿面温度称为本体温度,用θM表示。该温度在齿面上各点为一常数。
本体温度的大小直接影响进入啮合区润滑油粘度,从而影响摩擦系数的大小、啮合区油膜厚度以及啮合区的润滑状态。因此,它不仅对齿面胶合有决定意义,而且会使齿面发生软化现象,从而影响到齿面接触疲劳强度。
可根据Blok的热网分析法,对整个齿轮体作出全面温度估计。也可以在齿面表层埋入热电偶或其它方法直接测出本体温度。
加权系数
加权系数C2是考虑积分平均温度θflaint和本体温度θM对胶合损伤的影响程度不同而引入的系数。可由试验得出,可近似取C2=1.5。
积分温度
积分温度θint可用下式表示:θint=θM+C2θflaint
式中,θM为本体温度,C2为加权系数,θflaint为积分平均温度。
胶合温度
齿面出现胶合失效的极限积分温度,称为胶合温度,用θsint表示。通常是根据试验结果得出的。对一种“油—材料”组合,胶合温度θsint为常数,它不随运转条件改变。
平均摩擦系数
齿廓各点的摩擦系数的平均值,称为平均摩擦系数,用μm表示。可近似用节点处的摩擦系数代替。也可按GB6413—86式(14)求得。
行星齿轮传动的强度计算特
关于渐开线行星齿轮传动的强度计算方法,目前尚无专门标准,一般都是套用普通渐开线圆柱齿轮传动强度计算方法。但是,行星齿轮传动有些影响齿轮强度的因素与一般定轴轮系齿轮传动不同,如行星轮数和均载机构性能对齿向载荷分布系数Kβ值的影响,行星轮间载荷不均衡系数Kρ对计算载荷的影响等。有关行星齿轮传动强度计算的具体问题,可参考马从谦等编著的《渐开线行星齿轮传动设计》,该书于1987年由机械工业出版社出版。
高速齿轮传动的强度计算特点
目前圆柱齿轮传动的最高转速已达10000r/min,圆周速度已超过250m/s。随着科学技术的发展,齿轮速度起来越高,速度分界也发生变化,如AGMA认为v>25m/s就算高速,而FZG则认为v>30m/s才算高速。
高速齿轮传动的特点是,当齿轮圆周速度越过某一极值后,必须考虑由于高速引起的动载荷、振动和发热对承载能力的影响。因此,对齿轮的材料、设计、制造与润滑提出了更高的要求。高速齿轮传动精度一般要求达到ISO的4~6级,特殊情况下要求2~3级。
高速齿轮传动承载能力计算应包括:齿根弯曲强度计算、齿面接触强度计算和齿面胶合强度计算。设计高速齿轮要花很多精力去考虑齿轮的制造精度和装配精度问题。高速齿轮传动设计的具体问题,可参考ISO/WG6/(瑞士—16)242E和萨本洁编著的《高速齿轮传动设计》,该书于1986年由机械工业出版社出版。
圆弧齿轮的强度计算特点
圆弧齿轮传动的受力分析与失效形式和渐开线斜斜齿圆柱齿轮相似。但圆弧齿轮的应力分析却比渐开线齿轮复杂,以致迄今尚无满意的强度计算方法。圆弧齿轮的接触强度高于渐开线齿轮。单圆弧齿轮的弯曲强度比渐开线齿轮略低。双圆弧齿轮的弯曲强度高于渐开线齿轮。关于圆弧齿轮的强度计算具体问题,可参考太原工学院齿轮研究室主编《圆弧齿轮》,该书于1980年由机械工业出版社出版。或按《机械工程手册》第32篇第3章圆弧齿轮强度计算公式进行设计计算,其公式表达形式和渐开线齿轮相仿,它适用于中、低速的67型单圆弧齿轮传动。
圆弧齿轮强度计算公式与渐开线齿轮不同之处有下列几点:
(1)因为圆弧齿轮跑合以后,理论瞬时接触线是沿着齿高方向的,接触线的长度与模数mn成正比。另外,重合度ε的整数部分με
说明每一瞬间至少有με条理论接触线在工作,所以在接触应力公式中有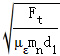 ;而渐开线齿轮的接触线是沿齿长方向的。接触线长度和工作齿宽b成正比,因而接触应力公式中有
;而渐开线齿轮的接触线是沿齿长方向的。接触线长度和工作齿宽b成正比,因而接触应力公式中有![]() 。
。
(2)圆弧齿轮螺旋角的大小,直接影响受载变形后的瞬时接触区的面积,面积越大,接触应力越疏散,最大接触应力下降,所以必需计入螺旋角的影响。根据赫兹公式推导,Zβ=√2tgβsinβ,其结果表明,曲率半径ρ对齿面接触强度过于敏感,因而根据分析和经验综合,取Zβ=√0.445sinβ;而渐开线齿轮的螺旋角影响系数为Zβ=√cosβ,可见两者的影响截然不同。
(3)接触应力公式中引入接触精度系数ZΩ,是考虑圆弧齿轮由于中心距误差和切深偏差而引起的接触迹偏离理论位置,对齿面接触强度的影响。
(4)渐开线齿轮计算载荷内计入端面载荷分配系数KFa,而圆弧齿轮由于εa=0,所以不需要考虑。
(5)圆弧齿轮轮齿上的载荷集中在一个较小的接触区域,因而沿齿长各处的弯曲应力是变化的。其最大弯曲应力与齿宽限没有直接关系,而与模数mn2成反比,这个结论符合材料力学中所讲的短而宽的悬臂梁在集中力作用下,应力和断面的关系。重合度的整数部分με是考虑每一瞬间至少有με对轮齿在啮合,分担着齿轮的圆周力Ft;而渐开线齿轮的齿根弯曲应力与bmn成反比。
(6)圆弧齿轮螺旋角的大小,直接影响受载变形后接触区宽度,接触区宽度愈宽,齿根弯曲应力也愈疏散,使齿根最大弯曲应力有所降低。但比齿面接触应力的敏感性小一些。这和渐开线齿轮相比影响是不同的。
开式齿轮的强度计算特点
开式齿轮的主要失效形式是齿面磨粒磨损。关于齿轮的磨损计算,目前尚无成熟的计算方法,一般可在计入磨损影响后,借用闭式齿轮强度计算公式进行计算。
开式齿轮一般只需许轮齿弯曲强度,为考虑磨损,应将求得的模数加大10%~20%。
蜗杆传动的强度计算特点
由于蜗杆传动的蜗轮齿形比较复杂,沿齿宽各截面上齿廓曲线形状各异,在同一节圆柱上,各截面的曲率半径也不相同,迄今还难以用解析法建立完善的齿面接触强度和齿根弯曲强度的表达式。即使计算式搞得很复杂,也难以说明其实际应力状态。因此,现有的蜗杆传动强度计算方法都是条件性的简化计算或经验公式。无论是齿面接触强度或齿根弯曲强度计算,都采用了仅包括蜗杆传动少数几个主要参数在内的简单表达式,用以指导设计实践的依据,主要依靠试验结果进行间接比较。换言之,通过试验手段将一批蜗杆副的具体参数条件代入该表达式,以获得不出现失效的极限应力或许用值,通过数学处理,制成图表供设计者使用。设计时则将设计蜗杆副的具体参数条件代入表达式得到计算应力值,再与试验所得极限值或许用值进行比较,计算过程中另用一些系数修正设计条件和试验条件之间存在的差异。综上所述,蜗杆传动强度计算方法有一定的相对性。目前没有一种满意的、统一的蜗杆传动强度计算方法(参考文献:孟惠荣,论近代蜗杆传动的类型、形成原理及发展方向,《煤矿机械》杂志,1981年第1,2,3,5期连载)。
蜗杆传动承载能力的计算方法
目前还没有统一的蜗杆传动承载能力计算方法。下面简要介绍几种蜗杆传动承载能力计算方法:
(1)按传动结构要求,选定中收距a,按经验公式计算蜗杆分度圆直径d1和m,按标准圆整后再分别验算齿面接触强度、齿根弯曲强度和发热功率。常见的有:AGMA公式(AGMA213.023;341.01;440.03)德国尼曼及DIN3976公式。
(2)按传动功率P1、转速n1及传动比i等直接查图线或系列表初定中心距a等尺寸。此法在欧洲和前苏联均有采用。
(3)根据传动P1及转速n1等,按扭转强度或刚度公式估计蜗杆直径,然后按经验公式确定蜗杆分度圆直径d1,再按经验公式算出中心距a等。最后再进行强度校核。如德国托马斯著《齿轮承载能力》(1973年中译本)。
(4)根据蜗杆发热功率安全准则,初定中心距a。如德国Kōhler/Rognitz,《机械零件》(1977)和Zirpke《齿轮》(1973)。
(5)根据齿面接触强度公式计算中心距a。这种方法是前苏联和国内《机械零件》常用的方法。
| 返回目录 | 上一页 |
 齿条 |
圆柱齿轮 |
圆锥齿轮 |
蜗轮蜗杆 |
非圆齿轮 |
特种齿轮
齿条 |
圆柱齿轮 |
圆锥齿轮 |
蜗轮蜗杆 |
非圆齿轮 |
特种齿轮首页 | 进口齿条 | 进口齿轮 | 齿轮标准 | 询价必读 | 齿轮知识 | 网站地图
电话:010-6492-5308 | 传真:010-6492-5744 | 邮件: sales@gearandrack.cn
2003-2012年北京正基元齿轮有限公司版权所有。本网站由北京正基元齿轮有限公司设计、制作、维护。
本网站上的任何内容,未经正基元公司的书面授权,均不得以任何方式复制、转载、或镜像,否则将追究其违权责任。